Interesting Statsitcal Problems in Interviews

Problem 1

If we have $n$ dice draws with a dice that has $k$ sides. Let $X_i$ to be the random variables that describes the number of times that the dice faces $i$. What is the correlation between $x_i$ and $x_j$ for $i\neq j$.

We first notice, $X_i$ are identitically distributed. Thus, the correlation between $X_i$ and $X_j$ does depend on $i$ and $j$ and they they have the same variance. Thus, we only need to calculate covariance first. We then notice

\[X_1+X_2 + \dots + X_k = n\]

Next we compute

\[\begin{aligned} &\text{Cov}[X_i, X_1+X_2+\dots + X_k] = \text{Cov}[X_i, n] =0 \\ &=\text{Cov}(X_i, X_i) + (k-1)\text{Cov}(x_i,x_j)\\ \end{aligned}\]

Thus, we find

\[(k-1)\text{Cov}(x_i,x_j) = - \text{Var}(X_i)\]

Thus,

\[\text{Cov}(x_i,x_j) = - \frac{\text{Var}(x_i)}{k-1}\]

Therefore, the correlation becomes

\[\text{Corr}(X_i,X_j) = \frac{\text{Cov}(X_i,X_j)}{\text{Var}(X_i)} = - \frac{1}{k-1}\]

Problem 2

With a set of 52 cards, we draw without replacement from the card. What is the expected number of draws to see the first Ace?

Counting down from the top of the deck of cards. Let $X_1$ be the number of cards before the first Ace. Let $X_2$ be the number of cards between the first and the second Ace. Let $X_3$ be the number of cards between the second and third Ace. Let $X_4$ be the number of cards between the third Ace and the fourth Ace. Finally, let $X_5$ be the number of cards between the fourth Ace and the bottom of the deck. We find

\[X_1+X_2+X_3+X_4+X_5 = 52-4 = 48\]

We also find the distribution of $X_i$’s are the same and thus,

\[5E[X_1] = 48\quad \Rightarrow \quad E[X_1] = \frac{48}{5}\]

Problem 3

A 2D random walk starts from $(1,1)$. If it will stop once it hits the $y$-axis. What is the probability that it will stop at the negative part of the $y$-axis?

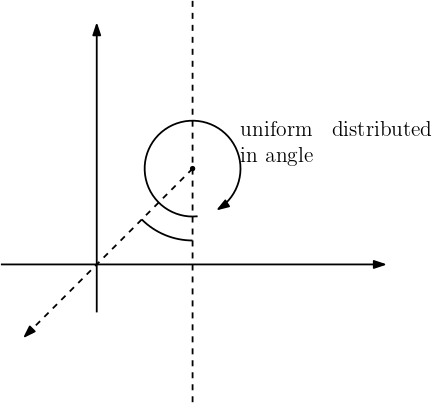
Notice the symmetry of the problem. In 2D random walk, the problem is symmetric. At a given time, it will be uniformly distributed in the direction respect to the starting point. Given it hits $y$-axis, it will be uniformly distributed around within the angle ($0$,$\pi$) with respect to the starting point. However, the probability of going to the negative part is the last $\pi/4$ angle. Thus, the probability of landing in the negative part of $y$-axis is $1/4$.

Problem 4

Give an example that two random variables are uncorrelated but dependent

Let $X = \sin(\tau)$ and $Y = \cos(\tau)$ and $\tau\sim U(0,2\pi)$. This is uncorrelated because, if we plot $(X,Y)$, it relys on the unit circle. If we run a linear regression on that, the line will have zero slope. Since correlation between $Y$ and $X$ is the $R^2$ score and it is zero in this case. They are dependent because, once we know $X$, $Y$ can only have at most two values.

Problem 5

How to uniformly generate points on a disc with radiu $R$?

If we label points by $(r,\theta)$, the probability density function of $(r,\theta)$ is

\[p(r,\theta)drd\theta = \frac{rd\theta dr }{\pi R^2} = \frac{d\theta}{2\pi} \cdot \frac{d r^2}{R^2} = p(\theta) p(r^2)\]

Thus, we uniformly generate $r^2$ in the interval $[0,R^2]$ and uniform generate $\theta$ from $[0,2\pi)$.

Problem 6

How do you use a standard normal distribution samples to estimate $\pi$ ?

This is different from using uniform to estimate $\pi$ where you try to create a monte carlo experiment in a unit square. But you could try to transform the normal to uniform by using the CDF. Here we could use the quantiles. The quantiles of normal samples are of uniform distribution and you could use the monte carlo to estimate the one quarter disk area in a unit square.

Here is another way: note that if $X\sim N(0,1)$, then \(E[|X|] = \int_{-\infty}^\infty |x| \frac{1}{\sqrt{2\pi}} e^{-x^2/2}dx = \sqrt{\frac{2}{\pi}} \int_0^\infty xe^{-x^2/2} dx = \sqrt{\frac{2}{\pi}}\) Therefore, we have \(\pi = \frac{2}{E[|X|]^2}\) Thus, if we are given a set of samples sampled from normal distribution, we could take 2/(np.mean(np.absolute(arr)))**2 as the estimation of $\pi$.

Problem 7

If we have two bags containing $n$ balls each and we call the bags as bag A and bag B. We also have a fair coin. Then we start a process: at each step, we toss the coin. If the head faces up, we draw a ball from A and if tail faces up, we draw a ball from bag B. We continue the process until I find I cannot draw a ball from the bag indicated by the coin. Then I open the other bag and I find there are $X$ balls remaining. Then the question is what is $E[X]$ ? What is the dependence on $n$? why?

First, we could calculate that analytically. Since the two bags are symmetric we could write \(E[X] = \frac{1}{2}E[X|\text{A is empty}] + \frac{1}{2} E[X|\text{B is empty}] = E[X|\text{A is empty}]\) Then if we draw $i$ balls from B before A is drain, then we totally draw $i +n$ balls with the last ball from $A$. Then there will be $n-i$ balls left in $B$. Thus, we could calculate this expectation as \(\begin{aligned} E[X|\text{A is empty}] &= \sum_{i=0}^{n-1} (n-i) {i+n-1 \choose i}\left(\frac{1}{2}\right)^{i+n-1} \\ &= \sum_{x = n}^{2n-1} (2n-x) { x-1 \choose n-1} \left(\frac{1}{2}\right)^{x-1} \\ &= 2n - 2n\sum_{x=n}^{2n-1} \frac{x!}{(x-n)!n!} \left(\frac{1}{2}\right)^x \\ &= 2n - 2n \left[\sum_{x=n}^{2n} \frac{x!}{(x-n)!n!}\left(\frac{1}{2}\right)^x - \frac{2n!}{n!n!} \left(\frac{1}{2}\right)^{2n} \right]\\ &= 2n {2n \choose n} \left(\frac{1}{2} \right)^{2n} \end{aligned}\) The power dependence on $n$ could be approximated using the exact formula but we can also argue from the other point of view.

Let $X_A - X_B$ be the number of left balls difference at each draw. Then we notice $X_A- X_B$ at each step can increase $1$ if we draw a ball from $B$ or decrease $1$ if we draw from $A$. Then $X_A-X_B$ forms a random walk. Also $E[X_A- X_B]$ will be zero at each step, since it is symmetric on A and B. Thus, at each step $i$ \(E[(X_A-X_B)^2] = \text{Var}(X_A- X_B) \sim i\) Also we know \(E[(X_A- X_B)^2] = E[X_A^2] + E[X_B^2] - 2E[X_AX_B]\) At final step, either $X_A$ or $X_B$ equal to $0$. if $X_B= 0$, then we have $E[X_A^2] \sim M$ where $M$ is the total number of steps used. But total number of steps is of order $n$ total number of balls. Thus, $E[X_A] \sim \sqrt{n}$.

Problem 8